s=a+b
d=a-b
Il motivo è presto detto: quello che noi sommiamo (o sottraiamo) non sono semplicemente dei numeri, ma sono degli enti geometrici nel piano, che oltre a possedere modulo hanno anche direzione e verso.
Concentrandoci sulla somma di due vettori, esistono due metodi per calcolarla:
1) mediante la "regola del parallelogramma", che consiste nell'ottenere il vettore somma a+b come diagonale di un parallelogramma avente per lati i vettori a e b;
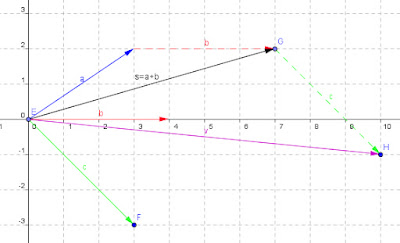
2) mediante il metodo "punta-coda" che consiste nel porre il vettore b sulla punta del vettore a e di unire la coda di quest'ultimo con la punta di b; il risultato sarà la somma dei vettori a e b.
Cosa fare, invece, se dobbiamo sommare tre vettori a, b e c?
Viene in aiuto una delle proprietà di cui gode la somma vettoriale: la proprietà commutativa.
(a+b)+c=a+(b+c)
1) in riferimento alla regola del parallelogramma, una volta ottenuto il vettore s = a+ b come diagonale del parallelogramma, se ne costruisce uno nuovo, con lati s e c; il risultato finale sarà la diagonale v del parallelogramma avente questi lati.
2) in riferimento al metodo "punta-coda", una volta ottenuto il vettore s = a + b, si ripete la procedura per il nuovo vettore c. Il risultato sarà il vettore v che unisce la coda del vettore a con la punta del vettore c traslato.



grazie 1000 !! bella spiegazione :)
RispondiEliminaSono lieto di aver soddisfatto la tua curiosità!
RispondiEliminaFabio
Sei single?
EliminaOttima spiegazione, grazie mille per quello che fate
RispondiEliminamolto più chiaro dei libri di scuola!
RispondiEliminase ci dite solo che cos'è un'equilibrante stiamo a posto
RispondiEliminaE' veramente una spiegazione chiarissima! Grazie!!
RispondiEliminaOttima spiegazione.
RispondiEliminaMi serviva proprio!
non è molto chiaro ma rileggendolo un po di volte si capisce
RispondiEliminaSei un prof.?
RispondiEliminagrazie mille per l'aiuto
RispondiEliminaIncredibile, avevo perso la speranza di trovare qualcuno che sapesse spiegare questa cosa! Grazie mille, davvero.
RispondiEliminaBuonasera, come applico la regola se ho due vettori nel secondo quadrante ed uno nel quarto?
RispondiEliminaBella spiegazione!
RispondiElimina