Somma di tre vettori.

In un precedente post si è discusso della somma di coordinate cartesiane. Questa operazione trova ampio utilizzo in Fisica, in particolare in riferimento alle operazioni di somma e di sottrazione di vettori, che danno come risultato un vettore

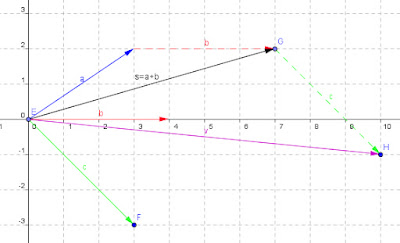
s=a+b

d=a-b

Questa operazione non coincide con la consueta somma algebrica di due numeri.
Il motivo è presto detto: quello che noi sommiamo (o sottraiamo) non sono semplicemente dei numeri, ma sono degli enti geometrici nel piano, che oltre a possedere modulo hanno anche direzione e verso.
Concentrandoci sulla somma di due vettori, esistono due metodi per calcolarla:
1) mediante la "regola del parallelogramma", che consiste nell'ottenere il vettore somma a+b come diagonale di un parallelogramma avente per lati i vettori a e b;

2) mediante il metodo "punta-coda" che consiste nel porre il vettore b sulla punta del vettore a e di unire la coda di quest'ultimo con la punta di b; il risultato sarà la somma dei vettori a e b.

Cosa fare, invece, se dobbiamo sommare tre vettori a, b e c?
Viene in aiuto una delle proprietà di cui gode la somma vettoriale: la proprietà commutativa.

(a+b)+c=a+(b+c)

questo vuol dire che i metodi visti nei punti 1 e 2 si possono iterare per un terzo vettore c. In particolare:
1) in riferimento alla regola del parallelogramma, una volta ottenuto il vettore s = a+ b come diagonale del parallelogramma, se ne costruisce uno nuovo, con lati s e c; il risultato finale sarà la diagonale v del parallelogramma avente questi lati.

2) in riferimento al metodo "punta-coda", una volta ottenuto il vettore s = a + b, si ripete la procedura per il nuovo vettore c. Il risultato sarà il vettore v che unisce la coda del vettore a con la punta del vettore c traslato.