Sottrazioni e divisioni immaginarie.

Abbiamo visto le operazioni di somma e moltiplicazione tra numeri complessi. Oggi trattiamo la sottrazione e la divisione, completando così le quattro operazioni.

Sottrarre due numeri complessi come  e  non è molto difficile, se si è ben capito qual'è la parte reale e la parte immaginaria: bisognerà sottrarre parte reale con parte reale e parte immaginaria con parte immaginaria.

Dividere due numeri complessi è, invece, un pò più difficile, e bisogna richiamare in causa un'operazione che già si svolge per semplificare le espressioni contenenti radicali al denominatore: la moltiplicazione per il complesso coniugato. Vediamo di capire.

Supponiamo di dover svolgere la seguente operazione:

Qual'è il quoziente di questa divisione?

Per rispondere a questa domanda, dobbiamo ricordarci che il termine i non è nient'altro che la radice quadrata di un numero negativo, quindi il sospetto che per svolgere questa operazione sia necessario semplificare usando il complesso coniugato del denominatore è forte. 

Il complesso coniugato di 3-i è 3+i, quindi possiamo moltiplicare numeratore e denominatore per l'espressione 

dove a numeratore e a denominatore compare il complesso coniugato di 3-i.

L'operazione di divisione tra numeri complessi si trasforma quindi in moltiplicare numeratore per numeratore e denominatore per denominatore; per quanto visto nel post precedente, la moltiplicazione tra due numeri complessi segue le regole tipiche del prodotto tra due binomi; in particolare, al denominatore avremo il prodotto della somma per la differenza di due binomi. Pertanto, il quoziente sarà:

Se osserviamo il risultato ottenuto, possiamo immediatamente notare come nel denominatore sia andata via la parte immaginaria e sia rimasta solo la parte reale (infatti, i^2 = -1). Nella divisione tra due numeri complessi, il denominatore del quoziente sarà costituito solo da un numero reale.

Un'altra osservazione importante è che il quoziente ottenuto è complessivamente dato da una parte reale (13/10) e una parte immaginaria (11i/10):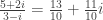 

Infine, affermando che 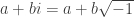, sarà sempre possibile semplificare espressioni del tipo , con .