Modelli matematici fuorvianti

Spesso si dice che la Matematica sia costituita da modelli che siano utili per comprendere appieno un dato argomento.

Di esempi di utilizzo di modelli nella Matematica ce ne sono a bizzeffe. Nelle previsioni meteo ci avvaliamo di dati che sono stati raccolti nel corso degli anni, costruiamo un modello, e con l'uso della teoria della probabilità prevediamo se pioverà o se ci sarà il sole in una data regione. Ma ancora, grazie ai modelli siamo in grado di fare delle previsioni come il transito di Venere sul sole che c'è stato il 5 di giugno, e il prossimo transito che sarà nel 2117!

Il transito di Venere sul Sole del 2004

Tuttavia, avere fede sempre e solo nei modelli matematici non basta. Per esempio, il grande matematico Fermat osservò che la sequenza

3, 5, 17, 257, 65537

è costituita da numeri primi. Secondo lui, questa sequenza può essere espressa mediante la formula 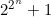, con n=0, 1, 2, 3, 4. Così, sarebbe possibile generare tutti i numeri primi per quei dati valori di n. Poi, arrivò il "ciclope" Eulero, che dimostrò che per n=5 si ottiene un numero non primo, per la precisione si ottiene .

Un altro classico esempio di modello fuorviante è dato dal numero massimo di partizioni che si possono creare in una circonferenza con dei segmenti. Con un solo segmento si creano due partizioni, cioè 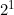 (figura 1); con tre segmenti si hanno quattro partizioni, cioè   (figura 2); con sei segmenti si ottengono 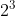 partizioni figura 3); e con 11 segmenti si otterrebbero  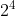partizioni (figura 4):

Verrebbe allora da dire che con 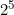 si otterrebbero ben 32 partizioni, ma la figura 5 ci dimostra impietosamente che così non è!

Questi esempi ci aiutano a comprendere qualcosa di opposto: non dobbiamo mai credere a ciò che osserviamo. Per questo motivo, in Matematica, esistono le dimostrazioni.